Generacja liczb pierwszych przez sprawdzanie podzielności

Definicja liczby pierwszej

Liczba pierwsza (ang. prime number) jest liczbą naturalną, która posiada dokładnie dwa różne podzielniki - liczbę 1 oraz samą siebie.

Przykłady liczb pierwszych:

2, 3, 5, 7, 11, 13, 17, 19, ...

Liczba 1 nie jest liczbą pierwszą. Co prawda dzieli się przez 1 i przez samą siebie, lecz jest to ten sam podzielnik a nie dwa różne, jak wymaga definicja.

Liczba zero również nie jest liczbą pierwszą, ponieważ nie dzieli się przez siebie samą.

Wynika z tego iż liczby pierwsze zawierają się w przedziale liczb naturalnych <2, ∞).

Sprawdzanie pierwszości:

Pierwszość (ang. primality) jest własnością liczby naturalnej, która mówi, iż dana liczba jest liczbą pierwszą. Sprawdzenie pierwszości polega na zbadaniu, czy dana liczba naturalna jest liczbą pierwszą. Podana na początku rozdziału definicja liczby pierwszej nie jest tutaj specjalnie przydatna - każda liczba naturalna dzieli się przez 1 i przez siebie samą.  Zatem musimy oprzeć algorytm na eliminacji liczb złożonych.

Liczba naturalna n jest liczbą złożoną, jeśli dzieli się bez reszty przez liczbę różną od 1 i różną od n.

Pierwszy algorytm będzie działał wg następującej idei:

Liczbę n będziemy próbowali dzielić przez kolejne liczby naturalne z przedziału od 2 do n-1. Jeśli któraś z tych liczb będzie dzieliła n bez reszty, to liczba n jest liczbą złożoną (zatem nie pierwszą) i algorytm możemy zakończyć z wynikiem negatywnym. Jeśli żadna z liczb od 2 do n-1 nie dzieli liczby n, to n jest liczbą pierwszą. Algorytm kończymy z wynikiem pozytywnym.

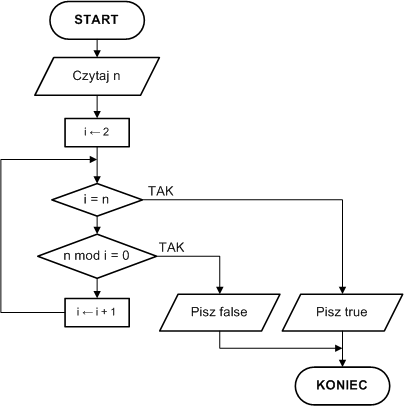
Algorytm sprawdzania pierwszości

Dane wejściowe:

n - liczby naturalna, której pierwszość badamy

Dane wyjściowe:

true - liczba n jest pierwsza
false - liczba n jest złożona

Dane pomocnicze:

i - kolejne podzielniki liczby n, i = 2, 3, ..., n-1

Lista kroków:

K01: Czytaj n
K01: Dla i =2,3,...,n -1  jeśli n mod i =0, to zakończ zwracając false
K02: Zakończ zwracając true

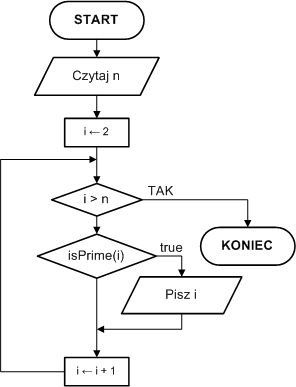
Schemat blokowy:

Generowanie liczb pierwszych

Gdy wiemy już jak sprawdzić pierwszość liczby naturalnej, możemy wykorzystać tę wiedzę do wygenerowania zadanej ilości liczb pierwszych lub liczb pierwszych z zadanego zakresu:

Generujemy odpowiednią ilość kolejnych liczb naturalnych. Każdą wygenerowaną liczbę naturalną testujemy na pierwszość. Jeśli test da wynik pozytywny, liczbę wypisujemy.

Algorytm generacji wszystkich liczb pierwszych z zakresu od 2 do n

Dane wejściowe:

n - liczba naturalna określająca górny kraniec przedziału generacji liczb pierwszych

Dane wyjściowe:

Kolejne liczby pierwsze leżące w przedziale od 2 do n.

Dane pomocnicze:

i - kolejne liczby naturalne z przedziału od 2 do n
isPrime(x) - funkcja zwracająca true, gdy x jest pierwsze, lub false, gdy x jest złożone

Lista kroków:

K01: Czytaj n
K01: Dla i = 2,3,...,n jeśli isPrime(i), to Pisz i
K02: Zakończ

Schemat blokowy: